曲线拟合 Curve Fitting
在上一篇文章中,我们讨论了图像的边缘检测,但是边缘检测完毕后存在一个问题就是噪点多,或者换句话说不光滑。
所以我们再增加一个步骤来使得图像轮廓更加平滑:曲线拟合。
原始图像–>(通过边缘检测)得到边缘图像–>(通过轮廓探测contour detector)得到坐标值(几何描述)
在进行正式的拟合之前,我们先回顾一下二维几何知识:向量
向量
向量知识中有个很重要的概念:点积。点积的意义主要是表征向量的相似性。值越大代表相似性越好。
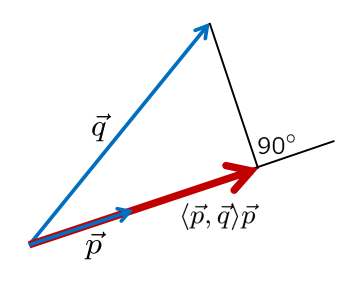
- 定义:⟨→p,→q⟩=p1q1+p2q2 其中p=(p1,p2), q=(q1,q2)
- 双线性:⟨α→p+β→r,γ→q+δ→s⟩=αγ⟨→p,→q⟩+αδ⟨→p,→s⟩+βγ⟨→r,→q⟩+βδ⟨→r,→s⟩
- 几何定义:⟨→p,→q⟩=|→p|⋅|→q|⋅cos∠(→p,→q)
- 拓展:
⟨→p,→p⟩=|→p|2, ⟨→p,→q⟩=0 if →p⊥→q
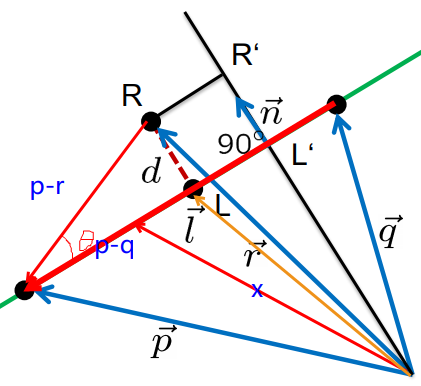
- 线和线段
我们可以把任意向量→x表示为→p−→q的某一段,我们用τ表示比例,即τ(→p−→q), τ∈[0,1]
那么我们可以得到→x=→p+τ(→p−→q)
化简得到:
→x=(1−τ)→p+τ→q,τ∈[0,1]
同理:→l也可通过以上表达:→l=(1−τ)→p+τ→q,τ∈[0,1]
→l−→r=d代表的向量
<→l−→r,→p−→q>=0 说明d和直线垂直
-
直线的一般形式:
|→n|=1,⟨→n,→q−→p⟩=0 ,|→n|为单位向量
⟨→n,→x⟩=⟨→n,(1−τ)→p+τ→q⟩=⟨→n,→p⟩+τ⟨→n,→q−→p⟩=⟨→n,→p⟩
0=⟨→n,→x⟩−⟨→n,→p⟩ =⟨→n,→x⟩+c (normal form)
-
点到直线的距离d:
d=||→l−→r‖=|⟨→n,→r⟩+c|
用单位向量表示一般向量:
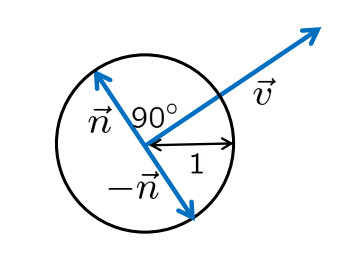
→v=(v1 v2)
→n=1|→v|(−v2 v1)
→|→n|=1,→n⊥→v
每个向量都可以用极坐标来表示:
→v=r⋅(cosϕsinϕ),r≥0,ϕ∈[0,2π) ϕ=atan2(v1,v2)通过点积可以来判断一个多边形是否面向摄像机(游戏开发中重要的一点);根据点积来计算光照效果(聚光);在计算机图学中进行方向性的判断
霍夫转换 Hough Transform
在边缘检测完毕后,我们通过霍夫转换,可以在边缘位图(edge bitmaps)中找到边缘线,每条线可以通过下面的式子来代替:
x⋅cosϕ+y⋅sinϕ+c=0
with 0∘≤ϕ<180∘ and c∈R
为什么可以这么表示呢?
因为在一般笛卡尔坐标系的直线表达式中,如y = kx+b,存在斜率为无穷大的情况,我们想办法找到一个类似于极坐标的表达方式。通过以上公式表达的方式我们称之为参数空间。在笛卡尔坐标系中的直线表达和 参数空间内的直线表达可以理解为一种映射,可以理解为同一种物体的不同维度的观察。
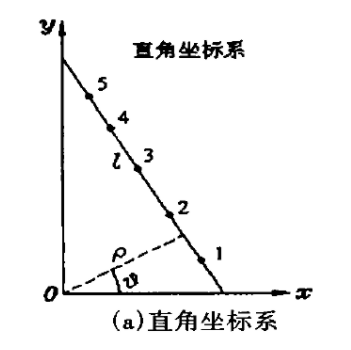
我们知道图中直线和它的垂线(虚线),一旦直线位置确定,那么其垂线的位置也是确定的。反之亦然。
如何找到这种映射关系呢?
假设有三个点A,B,C我们要判断其是否共线,这里我们假设其共线。

这条线的方程为
y=−x+2围绕A点可以做无数条直线,B、C同理。那么如果说其中的某三条线重合了,说明ABC共线。
那么这三条线的极坐标表示也是一样的,在参数空间内就相交于一点。
那么围绕A点扫描的所有直线的表达式为:
f=0×sinθ+2×cosθ,θ∈[0,π]围绕B点扫描的所有直线表达式为:
f=2×sinθ+0×cosθ,θ∈[0,π]围绕C点扫描的所有直线表达式为:
f=4×sinθ−2×cosθ,θ∈[0,π]然后做出函数图像,我们发现,三个函数交于
(π4,√2)我们现在知道了,他们相交的直线是以辐角为45°,幅值为√2的直线,大家再看笛卡尔坐标系中的直线位置,就明白了其映射关系。大家可以使用其他值作为例子进行体会。

霍夫转换的基本步骤
- 根据边缘线在参考空间中计算或者画出正弦曲线
- 计算交点
值得注意的是,在现实图像处理中,交点并不唯一。(多条线混合在一起)
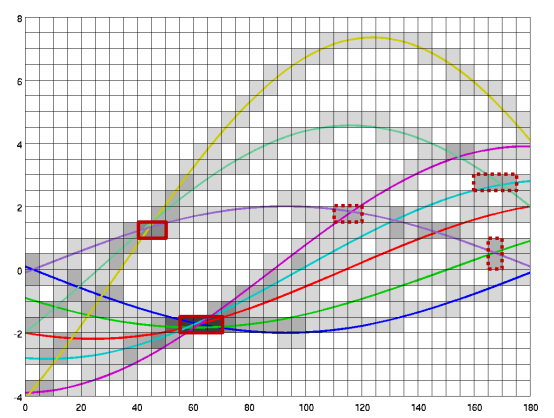
所以我们只能在高密度的区域中进行找点:
- 使用离散累加器单元阵列;
- 对每个单元计算正弦曲线穿过的数量;
- 在累加器阵列中进行局部最大值处理(根据线的参数)
有点类似我们小时候画三角形的垂直平分线,画完后交不到一点,我们用铅笔继续涂黑。
在许多边缘上的许多边缘点的霍夫变换
- 用0初始化具有足够精度的累加器阵列
- 使得所有满足线方程的累加器单元增加计数(有点拗口,就是计数)
- 在累加器中找到局部最大值(图像中最主要的参数)
在找到线参数后,可以将离线距离小的边缘像素分配到边缘线上。
但需要做两个工作:1. 确定线的起点和终点。2. 确定允许最大尺寸的间隙。
霍夫变换的性质
- 结果取决于累积器数组的大小和精度
- 在实践中,确定累积器阵列中的重要峰值可能是困难的
- 梯度方向被忽略
- 累加器数组在”自然场景“中溢出(我猜是计算量过大)
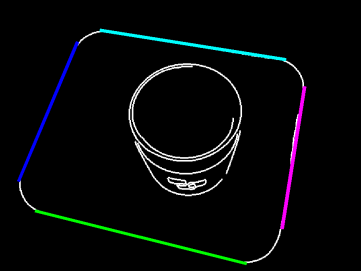
上图是一张经过霍夫变换后的图,在图中我们可以知道,圆弧部分并没有找到。
边缘追踪 Edge following
鉴于霍夫变换的缺点,我们可以通过另一条路线:
边缘检测edge detection–>边缘追踪edge following–>线段分割polyline segmentation–>直线拟合 line fitting
边缘追踪大体思路
- 边缘检测器产生具有边缘像素的位图
- 收集所有边缘像素并按拓扑顺序链接它们
- 使用梯度信息(如果可用)进行链接
- 结果:描述轮廓线的边缘像素列表
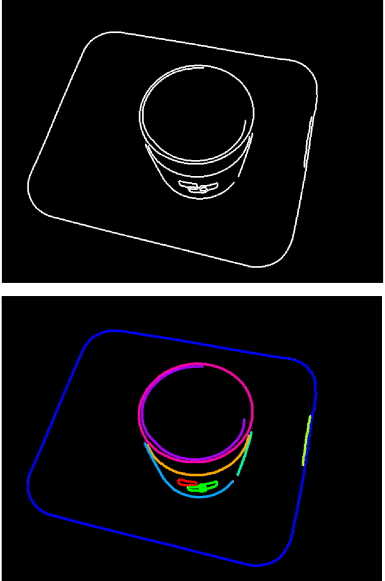
直线分割 Polyline Segmentation
边缘跟踪产生了有序的像素列表,但这些像素列表并不会主动或者自动的生成连线用以表示轮廓,所以我们的任务就是:细分像列表,使子列表可以用线段表示。
这里有很多的算法,我们只考虑Ramer Douglas Peucker算法,道格拉斯-普克算法
道格拉斯-普克算法的基本思路
在最远的顶点进行递归细分折线
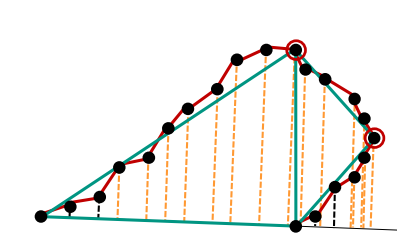
- 从第一个点到最后一个点连成线
- 计算各像素到线的距离
- 若最大的距离大于容差(自己定义的),则在最远的顶点打破边缘列表,并将算法再次应用到两个子列表(列表被打破成两个)
总体思想就是递归思想。
直线拟合
由于折线分割和霍夫转换的结果不一定是最优的,所以我们提出直线拟合的算法。
很容易想到我们以前中学学过的直线拟合算法:最小二乘法
最小二乘法
在这里我们做一下基本的回顾和加深:
在前面的二维几何知识回顾里,我们知道了:
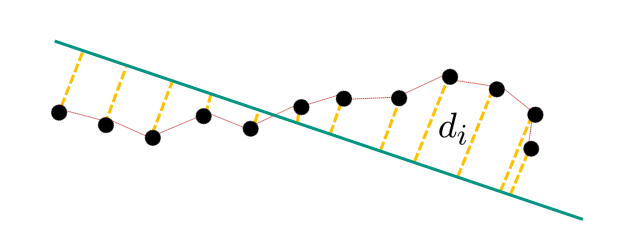
如果给定了我们单位向量→n以及c, 我们可以计算→xi到直线的距离为
di=|⟨→n,→xi⟩+c|我们找到最小的di
不想看推到过程的可以跳到后面,看结论就行了。
完全最小二乘法:
minimise→n,cN∑i=1d2i subject to ⟨→n,→n⟩=1拉格朗日算子(自行回顾高等数学)
L(→n,c,λ)=N∑i=1d2i−λ(⟨→n,→n⟩−1) =N∑i=1(⟨→n,→xi⟩+c)2−λ(⟨→n,→n⟩−1)对c进行归零偏导
∂L∂c=2N∑i=1⟨→n,→xi⟩+2Nc!=0 →c=−1NN∑i=1⟨→n,→xi⟩=−1N⟨→n,N∑i=1→xi⟩=−⟨→n,1NN∑i=1→xi⟩对n1和n2归零偏导
∂L∂n1=2(∑ix2i,1)n1+2(∑ixi,1xi,2)n2+2(∑ixi,1)c−2λn1!=0 ∂L∂n2=2(∑ixi,1xi,2)n1+2(∑ix2i,2)n2+2(∑ixi,2)c−2λn2!=0替换:
(∑ix2i,1−1N(∑ixi,1)2)⏟=:αn1+(∑ixi,1xi,2−1N∑ixi,1∑ixi,2)⏟=:βn2=λn1 (∑ixi,1xi,2−1N∑ixi,1∑ixi,2)⏟=βn1+(∑ix2i,2−1N(∑ixi,2)2)n2=λn2⏟=γ用矩阵形式表示:
(αββγ)→n=λ→nλ是特征值,→n是特征向量
两种结果:
λ1≥λ2≥0λ2–>最小距离, λ1–>最大距离。
最小二乘法的步骤
-
从所有的边缘像素中计算: ∑ixi,1,∑ixi,2,∑ix2i,1,∑ix2i,2,∑ixi,1xi,2
- 计算矩阵 (αβ βγ) 的特征向量和特征值,取较小的特征值
- 根据→n计算c
- 如果您对线段感兴趣,请根据投影在线上的边缘像素确定起点和终点。
直线估计
稳健性
稳健性是指在估计过程中,拟合过程中,对模型误差的不敏感性。
在最小二乘法中,如果出现异常值,那么拟合的直线很容易被带偏。
然而异常值在机器视觉中经常出现。
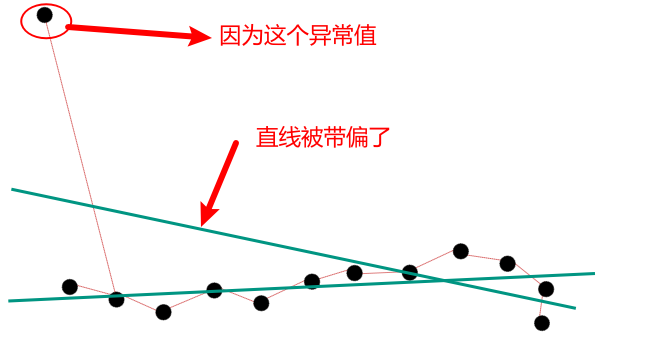
现在有两个思路:
- 减少总异常值的影响–> M估计,M Estimator
- 忽略异常值–>RANSAC算法
M估计
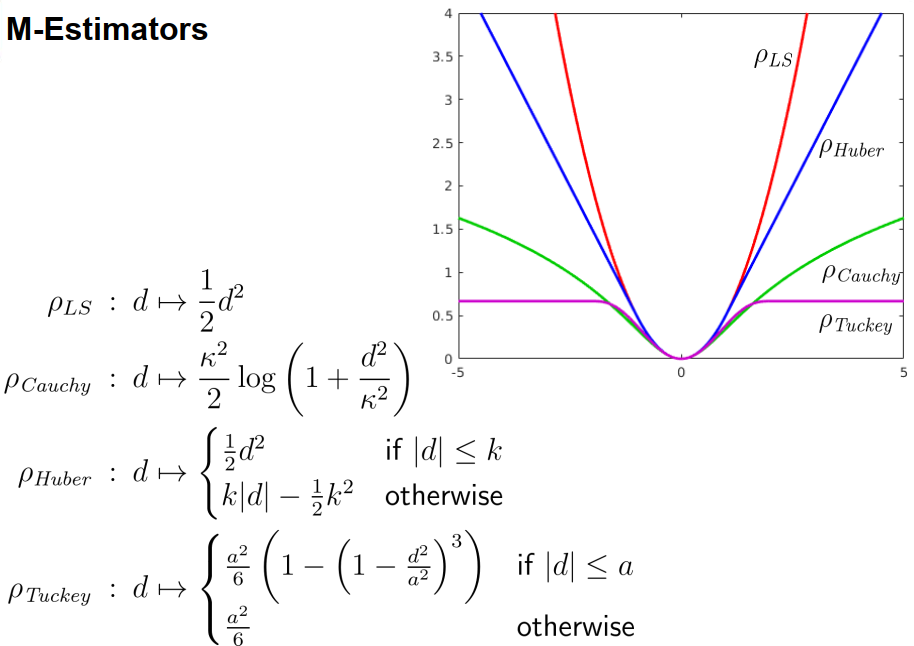
其中ρ越小,越靠近直线。
RANSAC随机抽样一致算法
一种通过使用观测到的数据点来估计数学模型参数的迭代方法
random sample consensus
RANSAC算法是一个学习的技巧,通过使用观测数据的随机样本来估计模型参数。RANSAC使用投票机制来寻找优化的拟合结果。每个数据元被用来投票一或多个模型。投票机制基于两点假设:
(1)噪音大的特征并不能一直单独为某个模型投票
(2)有足够多的特征来拟合一个好的模型
思路
搜索通过尽可能多点靠近的线
算法
- 随机选择两点
- 拟合
- 检查公差带之外的点数(异常值的数量)
- 用不同的点重复这个过程
- 选择异常值数量最少的线
